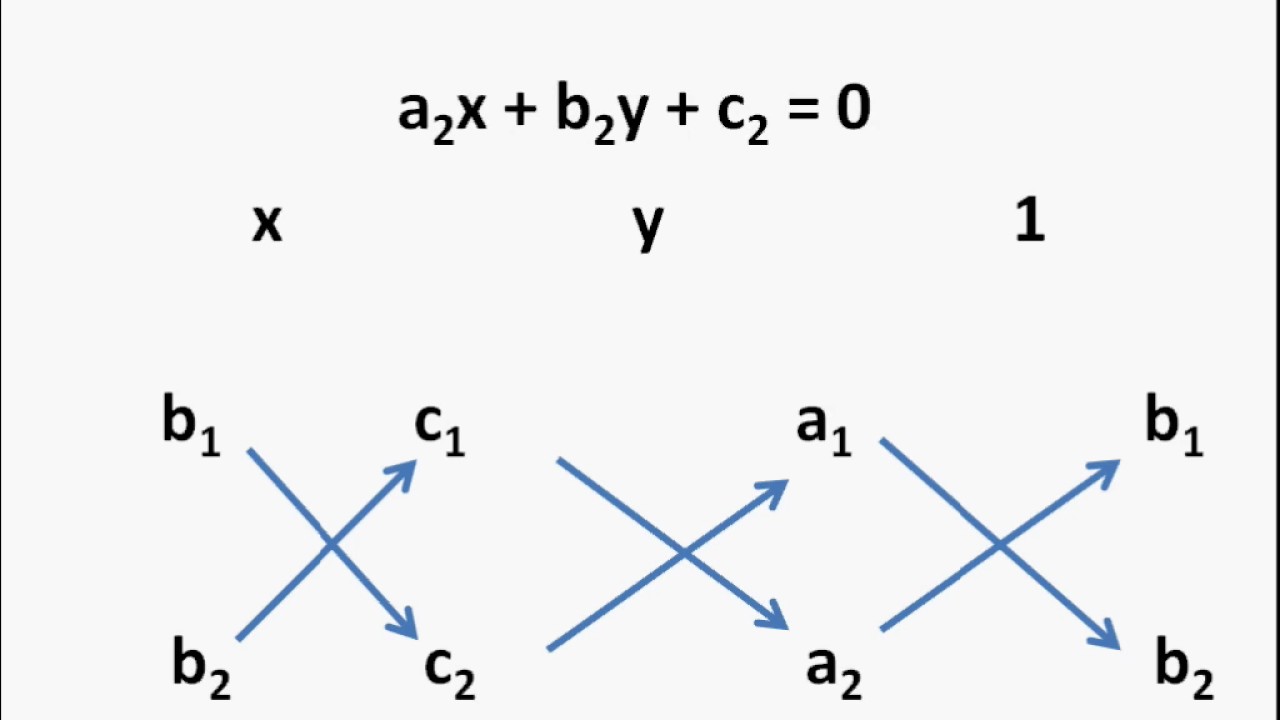
When we multiply the numerator on the left-hand side of the equation with the denominator of the right-hand side of the equation, we get the product of the numerator and denominator. This kind of equation solving method is known as the cross multiplication method for solving equations.
Problem number 1: Solve 4/y = 2 / 8.
Here, the relationship between 4 and y is of division. Here, we will use the cross multiplication method to multiply 4 by 8 and divide it by 2. At the same time, we will take y to the upper side of the numerator.
4 X 8 / 2 = y
32 / 2 = y
16 = y
Hence, the value of y is 16.
Note:
Whenever we shift any term from the left-hand side to the right-hand side of the equation or any term from the right-hand side to the left-hand side of the equation, the sign of the term of the equation will change.
This means that the +ve sign will become the -ve sign and a -ve sign will become the +ve sign. The multiplication (X) sign will become the division (÷) sign and the division ÷ sign will become the X sign.
Problem sum 1:
5a — 1 4
———- = ——
5a + 4 5
Solution:
Here, ( 5a — 1 ) will be multiplied by 5, and (5a +4) will be multiplied by 4.
We are using a cross multiplication method for solving the equations.
(5a - 1) X 5 = (5a + 4) X 4
On the LHS side, we will multiply 5 with both 5a and -1.
On the RHS side, we will multiply 4 with both 5a and +4
25a - 5 = 20a + 16 (we will shift places of like terms )
25a - 20a = 16 + 5
5a = 21
a = 21/5
So, the value of a = 21/5.
Problem Sum 2: The denominator of a rational number is greater than its numerator by five. If the numerator is increased by 15 and the denominator is decreased by two, the number obtained will be three upon nine. Find the rational number.
Solution:
Let the numerator of the equation is m
The denominator of the equation is greater by numerator by five = m + 5
So the fraction will be (m / m+ 5 )
Now, we will frame the equation.
It is given that the numerator is increased by 15 and the denominator is decreased by 2
So, the given equation will be:
m + 15 3
——————- = ——-
(m + 5) — 2 9
m + 15 1
—————— = ————
m + 5 — 2 3
m + 15 1
———— = ————-
m + 3 3
(m + 15 ) x 3 = 1 x ( m + 3)
3m + 45 = m + 3…….. (Eq 1)
3m - m = 3 - 45
2m = - 42
m = - 42/2
m = - 21
So form eq 1, the numerator will be m + 15 = (- 21) +15 = - 21 +15 = - 7
The denominator will be (m + 5) - 2 = m + 3 = - 21 + 3 = -18
So the fraction will be - 7 / -18
ie = ⅞